Gravity Calculations over Bodies with more Complex Shapes
Although it is possible to derive analytic expressions for the computation of the gravitational acceleration over additional bodies with simple shapes (cylinders, slabs, etc.), we already have enough information to describe a general scheme for computing gravity anomalies over bodies with these and more complex shapes. The basis for this computation lies in the approximation of a complex body as a distribution of point masses.
Previously, we derived the vertical component of the gravitational acceleration due to a point mass with mass m as
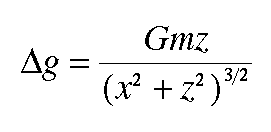
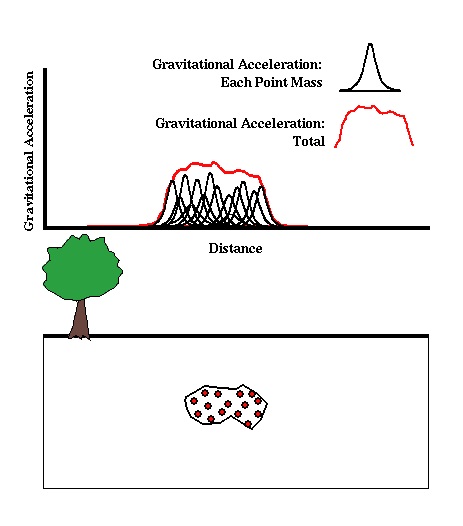
We can approximate the body with complex shape as a distribution of point masses. The gravitational attraction of the body is then nothing more than the sum of the gravitational attractions of all of the individual point masses as illustrated below.
In mathematical notation, this sum can be written as
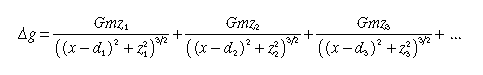
where z represents the depth of burial of each point mass, d represents the horizontal position of each point mass, and x represents the horizontal position of the observation point. Only the first three terms have been written in this equation. There is, in actuality, one term in this expression for each point mass. If there are N point masses, this equation can be written more compactly as
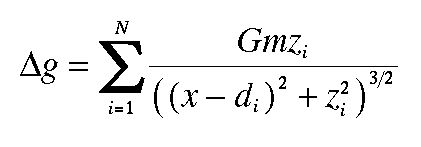
For more detailed information on the computation of gravity anomalies over complex two- and three- dimensional shapes look at the following references.
- Talwani, Worzel, and Landisman, Rapid Gravity Computations for Two-Dimensional Bodies with Application to the Mendocino Submarine Fraction Zone, Journal Geophysical Research, 64, 49-59, 1959.
- Talwani, Manik, and Ewing, Rapid Computation of Gravitational Attraction of Three-Dimensional Bodies of Arbitrary Shape, Geophysics, 25, 203-225, 1960.
Gravity
- Overviewpg 12
- -Temporal Based Variations-
- Instrument Driftpg 13
- Tidespg 14
- A Correction Strategy for Instrument Drift and Tidespg 15
- Tidal and Drift Corrections: A Field Procedurepg 16
- Tidal and Drift Corrections: Data Reductionpg 17
- -Spatial Based Variations-
- Latitude Dependent Changes in Gravitational Accelerationpg 18
- Correcting for Latitude Dependent Changespg 19
- Vari. in Gravitational Acceleration Due to Changes in Elevationpg 20
- Accounting for Elevation Vari.: The Free-Air Correctionpg 21
- Variations in Gravity Due to Excess Masspg 22
- Correcting for Excess Mass: The Bouguer Slab Correctionpg 23
- Vari. in Gravity Due to Nearby Topographypg 24
- Terrain Correctionspg 25
- Summary of Gravity Typespg 26