Model Indeterminancy

We have now derived the gravitational attraction associated with a simple spherical body. The vertical component of this attraction was shown to be equal to:

Notice that our expression for the gravitational acceleration over a sphere contains a term that describes the physical parameters of the spherical body; its radius, R, and its density contrast, 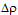, in the form

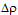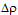R and are two of the parameters describing the sphere that we would like to be able to determine from our gravity observations (the third is the depth to the center of the sphere z). That is, we would like to compute predicted gravitational accelerations given estimates of R and , compare these to those that were observed, and then vary R and 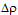until the predicted acceleration matches the observed acceleration.

This sounds simple enough, but there is a significant problem: there is an infinite number of combinations of R and 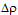that produce exactly the same gravitational acceleration! For example, let's assume that we have found values for R and 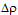that fit our observations such that

Any other combination of values for R and 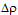will also fit the observations as long as R cubed times 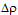equals 31.25. Examples of the gravity observations produced by four of these solutions are shown below.

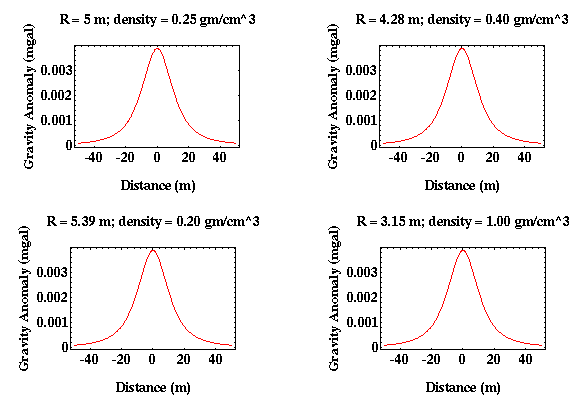
Our inability to uniquely resolve parameters describing a model of the earth from geophysical observations is not unique to the gravity method but is present in all geophysical methods. This is referred to using a variety of expressions: Model Interminancy, Model Equivalence, and Nonuniqueness to name a few. No matter what it is called, it always means the same thing; a particular geophysical method can not uniquely define the geologic structure underlying the survey. Another way of thinking about this problem is to realize that a model of the geologic structure can uniquely define the gravitational field over the structure. The gravitational field, however, can not uniquely define the geologic structure that produced it.

If this is the case, how do we determine which model is correct? To do this we must incorporate additional observations on which to base our interpretation. These additional observations presumably will limit the range of acceptable models we should consider when interpreting our gravity observations. These observations could include geologic observations or observations from different types of geophysical surveys.

❮❮ Previous Next ❯❯