Variations in Gravity Due to Nearby Topography

Although the slab correction described previously adequately describes the gravitational variations caused by gentle topographic variations (those that can be approximated by a slab), it does not adequately address the gravitational variations associated with extremes in topography near an observation point. Consider the gravitational acceleration observed at point B shown in the figure below.

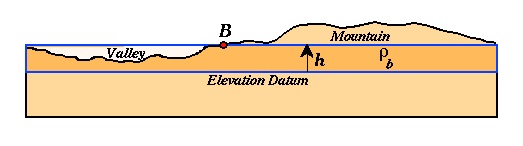
In applying the slab correction to observation point B, we remove the effect of the mass surrounded by the blue rectangle. Note, however, that in applying this correction in the presence of a valley to the left of point B, we have accounted for too much mass because the valley actually contains no material. Thus, a small adjustment must be added back into our Bouguer corrected gravity to account for the mass that was removed as part of the valley and, therefore, actually didn't exist.

The mass associated with the nearby mountain is not included in our Bouguer correction. The presence of the mountain acts as an upward directed gravitational acceleration. Therefore, because the mountain is near our observation point, we observe a smaller gravitational acceleration directed downward than we would if the mountain were not there. Like the valley, we must add a small adjustment to our Bouguer corrected gravity to account for the mass of the mountain.

These small adjustments are referred to as Terrain Corrections. As noted above, Terrain Corrections are always positive in value. To compute these corrections, we are going to need to be able to estimate the mass of the mountain and the excess mass of the valley that was included in the Bouguer Corrections. These masses can be computed if we know the volume of each of these features and their average densities.

❮❮ Previous Next ❯❯