Gravity Anomaly Over a Buried Sphere

It can be shown that the gravitational attraction of a spherical body of finite size and mass m is identical to that of a point mass with the same mass m. Therefore, the expression derived on the previous page for the gravitational acceleration over a point mass

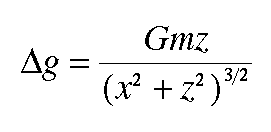
also represents the gravitational acceleration over a buried sphere. For application with a spherical body, it is convenient to rewrite the mass, m, in terms of the volume and the density contrast of the sphere with the surrounding earth using

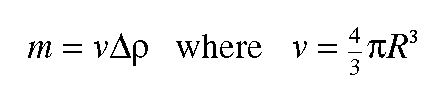
where v is the volume of the sphere, 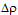is the density contrast of the sphere with the surrounding rock, and R is the radius of the sphere. Thus, the gravitational acceleration over a buried sphere can be written as

Although this expression appears to be more complex than that used to describe the gravitational acceleration over a buried sphere, the complexity arises only because we've replaced m with a term that has more elements. In form, this expression is still identical to the gravitational acceleration over a buried point mass.

❮❮ Previous Next ❯❯