Correcting for Excess Mass: The Bouguer Slab Correction

Although there are obvious shortcomings to the simple slab approximation to elevation and mass differences below gravity stations, it has two distinct advantages over more complex (realistic) models.

• Because the model is so simple, it is rather easy to construct predictions of the gravity produced by it and make an initial, first-order correction to the gravity observations for elevation and excess mass.
• Because gravitational acceleration varies as one over the distance to the source of the anomaly squared and because we only measure the vertical component of gravity, most of the contributions to the gravity anomalies we observe on our gravimeter are directly under the meter and rather close to the meter. Thus, the flat slab assumption can adequately describe much of the gravity anomalies associated with excess mass and elevation.

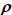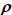Corrections based on this simple slab approximation are referred to as the Bouguer Slab Correction. It can be shown that the vertical gravitational acceleration associated with a flat slab can be written simply as -0.04193h. Where the correction is given in mgals, is the density of the slab in gm/cm^3, and h is the elevation difference in meters between the observation point and elevation datum. h is positive for observation points above the datum level and negative for observation points below the datum level.

Notice that the sign of the Bouguer Slab Correction makes sense. If an observation point is at a higher elevation than the datum, there is excess mass below the observation point that wouldn't be there if we were able to make all of our observations at the datum elevation. Thus, our gravity reading is larger due to the excess mass, and we would therefore have to subtract a factor to move the observation point back down to the datum. Notice that the sign of this correction is opposite to that used for the elevation correction.

Also notice that to apply the Bouguer Slab correction we need to know the elevations of all of the observation points and the density of the slab used to approximate the excess mass. In choosing a density, use an average density for the rocks in the survey area. For a density of 2.67 gm/cm^3, the Bouguer Slab Correction is about 0.11 mgals/m.

❮❮ Previous Next ❯❯