Gravitational Force

Geophysical interpretations from gravity surveys are based on the mutual attraction experienced between two masses* as first expressed by Isaac Newton in his classic work Philosophiae naturalis principa mathematica (The mathematical principles of natural philosophy).

Newton's law of gravitation states that the mutual attractive force between two point masses**, m₁ and m₂, is proportional to one over the square of the distance between them. The constant of proportionality is usually specified as G, the gravitational constant. Thus, we usually see the law of gravitation written as shown to the right where F is the force of attraction, G is the gravitational constant, and r is the distance between the two masses, m₁ and m₂.

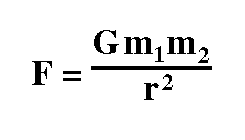
*As described on the next page, mass is formally defined as the proportionality constant relating the force applied to a body and the accleration the body undergoes as given by Newton's second law, usually written as F=ma. Therefore, mass is given as m=F/a and has the units of force over acceleration.

**A point mass specifies a body that has very small physical dimensions. That is, the mass can be considered to be concentrated at a single point.

❮❮ Seismology Next ❯❯