Latitude Dependent Changes in Gravitational Acceleration

Two features of the earth's large-scale structure and dynamics affect our gravity observations: its shape and its rotation. To examine these effects, let's consider slicing the earth from the north to the south pole. Our slice will be perpendicular to the equator and will follow a line of constant longitude between the poles.

• Shape - To a first-order approximation, the shape of the earth through this slice is elliptical, with the widest portion of the ellipse aligning with the equator. This model for the earth's shape was first proposed by Isaac Newton in 1687. Newton based his assessment of the earth's shape on a set of observations provided to him by a friend, named Richer, who happened to be a navigator on a ship. Richer observed that a pendulum clock that ran accurately in London consistently lost 2 minutes a day near the equator. Newton used this observation to estimate the difference in the radius of the earth measured at the equator from that measured at one of the poles and came remarkably close to the currently accepted values.

  

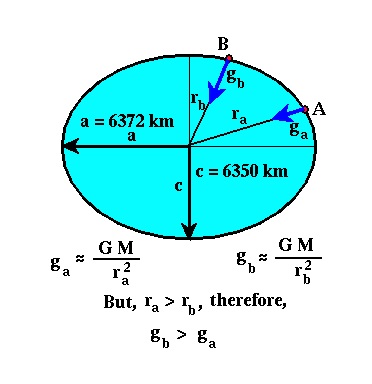
  Although the difference in earth radii measured at the poles and at the equator is only 22 km (this value represents a change in earth radius of only 0.3%), this, in conjunction with the earth's rotation, can produce a measurable change in the gravitational acceleration with latitude. Because this produces a spatially varying change in the gravitational acceleration, it is possible to confuse this change with a change produced by local geologic structure. Fortunately, it is a relatively simple matter to correct our gravitational observations for the change in acceleration produced by the earth's elliptical shape and rotation.

  To first order*, the elliptical shape of the earth causes the gravitational acceleration to vary with latitude because the distance between the gravimeter and the earth's center varies with latitude. As discussed previously, the magnitude of the gravitational acceleration changes as one over the distance from the center of mass of the earth to the gravimeter squared. Thus, qualitatively, we would expect the gravitational acceleration to be smaller at the equator than at the poles, because the surface of the earth is farther from the earth's center at the equator than it is at the poles.

• Rotation - In addition to shape, the fact that the earth is rotating also causes a change in the gravitational acceleration with latitude. This affect is related to the fact that our gravimeter is rotating with the earth as we make our gravity reading. Because the earth rotates on an axis passing through the poles at a rate of once a day and our gravimeter is resting on the earth as the reading is made, the gravity reading contains information related to the earth's rotation.

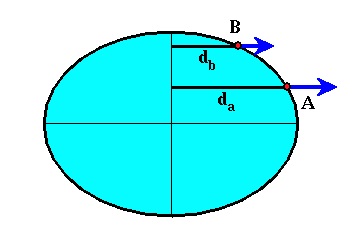
  We know that if a body rotates, it experiences an outward directed force known as a centrifugal force. The size of this force is proportional to the distance from the axis of rotation and the rate at which the rotation is occurring. For our gravimeter located on the surface of the earth, the rate of rotation does not vary with position, but the distance between the rotational axis and the gravity meter does vary. The size of the centrifugal force is relatively large at the equator and goes to zero at the poles. The direction this force acts is always away from the axis of rotation. Therefore, this force acts to reduce the gravitational acceleration we would observe at any point on the earth, from that which would be observed if the earth were not rotating.

*You should have noticed by now that expressions like "to first order" or "to a first order approximation" have been used rather frequently in this discussion. But, what do they mean? Usually, this implies that when considering a specific phenomena that could have several root causes, we are considering only those that are the most important.

❮❮ Previous Next ❯❯