A Simple Model

Consider the variation in gravitational acceleration that would be observed over a simple model. For this model, let's assume that the only variation in density in the subsurface is due to the presence of a small ore body. Let the ore body have a spherical shape with a radius of 10 meters, buried at a depth of 25 meters below the surface, and with a density contrast to the surrounding rocks of 0.5 grams per centimeter cubed. From the table of rock densities , notice that the chosen density contrast is actually fairly large. The specifics of how the gravitational acceleration was computed are not, at this time, important.

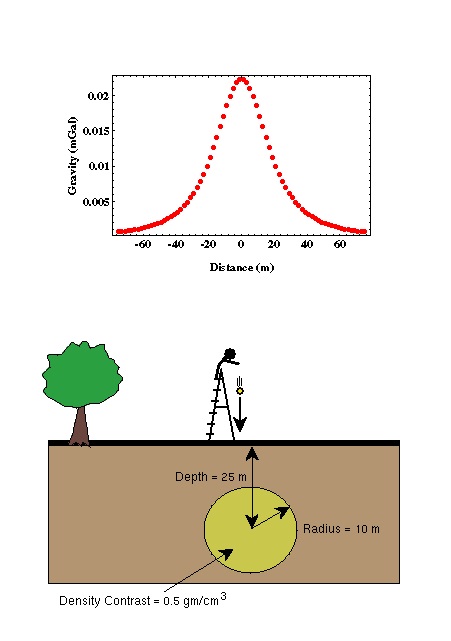
There are several things to notice about the gravity anomaly* produced by this structure.

• The gravity anomaly produced by a buried sphere is symmetric about the center of the sphere.
• The maximum value of the anomaly is quite small. For this example, 0.025 mgals.
• The magnitude of the gravity anomaly approaches zero at small (~60 meters) horizontal distances away from the center of the sphere.

Later, we will explore how the size and shape of the gravity anomaly is affected by the model parameters such as the radius of the ore body, its density contrast, and its depth of burial. At this time, simply note that the gravity anomaly produced by this reasonably-sized ore body is small. When compared to the gravitational acceleration produced by the earth as a whole, 980,000 mgals, the anomaly produced by the ore body represents a change in the gravitational field of only 1 part in 40 million.

Clearly, a variation in gravity this small is going to be difficult to measure. Also, factors other than geologic structure might produce variations in the observed gravitational acceleration that are as large, if not larger.

---

*We will often use the term gravity anomaly to describe variations in the background gravity field produced by local geologic structure or a model of local geologic structure

---

❮❮ Previous Next ❯❯