Introduction and Statement of Problem

In designing a gravity survey for a particular application, there are several design parameters that must be chosen or known: gravity station spacing, location of the base station, time interval between base station reoccupations, and the level of reading error inherent to the basic observations.

This exercise focuses on assessing the latter two parameters: base station reoccupation interval and the level of reading error inherent to the observations.

• Reoccupation Interval - The time interval between subsequent gravity readings at the base station is an important parameter in controlling the effectiveness of the drift and tidal corrections computed from the field observations. There is an inherent trade-off between survey cost and survey accuracy in choosing this parameter.
  • Short Time Intervals - The use of a short time interval between subsequent base station readings will produce better estimates of the tidal and drift components of the observed field so that they can be more accurately removed. More frequent base station readings, however, allow for fewer gravity stations to be surveyed during a given time period. Thus, the smaller the base station reoccupation interval, the longer it takes to complete a given survey, and the more the survey costs.
  • Long Time Intervals - By reoccupying the base station less frequently, more gravity stations can be surveyed during a given time period. Hence, the cost of the survey can be reduced. If the time interval between subsequent base station readings is too long, however, the drift and the tidal component of the observed field can not be correctly removed from the data set. Thus, residual* drift and tides will corrupt the final data.
  
  

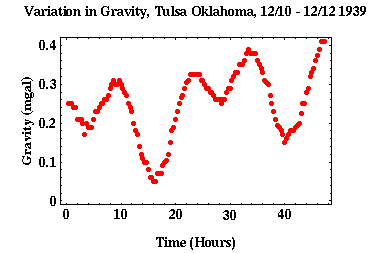
  To estimate what the optimum time interval between subsequent base station reoccupations given the cost/accuracy tradeoff, we will use the earth tide data that was presented in the notes and is reproduced to the right. Given that this data set was acquired at a single location, it directly shows the gravitational variation resulting from tides and instrument drift without geologic complications. Thus, we can use this data set to estimate the optimal base station reoccupation interval. In this case, as is the case with choosing parameters for all geophysical surveys, optimal depends on the specifics of the target that is being sought.

• Observation Resolution - All measures involve an inherent error. That is, no measure can be made with absolute accuracy. This is indeed true with measurements of the Earth's gravitational acceleration. These errors could be due to inaccurate leveling of the instrument, motion of the instrument caused by traffic, microseisms, or people walking about, or errors in reading the output of the instrument. In the tidal data set shown above, for example, the author** reported a reading error of 0.01 to 0.02 mgal. This level of reading error is quite good, being near the resolution possible with the instrumentation. Exploration gravity surveys usually have reading errors larger than this. The exception, surveys that are designed to minimize this error, are referred to as micro-gravity surveys.

  One common method of reducing these errors is to make multiple readings at a single location and averaging the result. If the errors associated with the readings are random, it can be shown that the reading error is reduced by the square root of the number of observations made.

  
  

  Thus, if the error associated with one reading is 0.02 mgals, averaging 4 readings will reduce the error to 0.01 mgals, averaging 16 readings will reduce the error to 0.005 mgals, etc. Notice, that because this technique requires multiple observations at each station, relying on reading averaging to reduce reading errors will increase the cost of the survey.

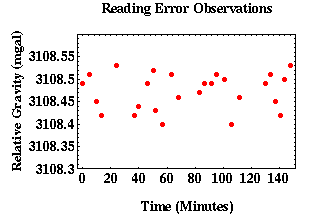
  Shown to the left is a series of gravity observations made at a single location by a novice gravity crew. We will use these observations to make conservative estimates of the errors inherent in our gravity observations. If there were no reading errors in this data set, we would expect all of the observations to lie approximately along a straight line. The slope of this line depends on where in the tidal cycle these observations were collected (Remember all of the observations will not have the same value because they will still contain an earth tide contribution).

Procedure

• Base Station Reoccupation Requirements - To complete this portion of the exercise you will need to download gravity data to your computer, import it into a spreadsheet, display the input data using the spreadsheet's display functions, perform a series of linear interpolations of the data, compute residual estimates between the estimated and actual tidal values, and derive an optimal base station reoccupation interval.
  
  To complete this portion of the exercise perform the following tasks:
  
  
  • Download tidal dataset to you machine (once redirected, right click the page and select "Save as.." to download the csv file). The first column in the data set is the hour at which the observation was made, and the second column is the relative gravity reading in mgals. The first line in the data set is a column label line. Columns are tab separated. When you click in the highlighted area above, a menu will be displayed asking you where you would like the file saved on your machine and what you would like to name it.
  • Import tidal.dat into your favorite spreadsheet.
  • Using the graphical features of your spreadsheet, plot the observed gravity versus time. Your plot should resemble the one displayed above.
  • Now, let's determine the effectiveness of using a base station reoccupation interval of 5 hours.
    • Using the spreadsheet's mathematical functions, create a third column of data linearly interpolating the observations between 0.33 and 5.33 hours, between 5.33 and 10.33 hours, etc. Continue up to 45.33 (do not worry about the last set of observations between 45.33 and 47.33 hours). These values now represent the tidal values you would have predicted given only base station observations made every 5 hours.
    • Test how good your predictions are by subtracting the values given in column 3 from the observed gravity values given in column 2. The result of this operation has to yield a zero every 5 hours. If it doesn't, you either did the linear interpolation or the subtraction wrong. At the intermediate times, these values represent the residual tidal affect that your interpolation did not correctly account for. If our tidal approximation is good, these residuals should all be small.
    • Plot column 4, the residuals, versus time.
    • To quantify the size of the residual, compute their root mean square (RMS) value. To compute the RMS of the residules, do the following: sum the squares of the residuals, divide by the number of residuals used in the sum (do not include the end points used to do the linear interpolation that have zero residual), and take the square root of the result.
    • Repeat these steps for base station reoccupation intervals of 4, 3, 2, 1, and 0.66 hours. For these shorter time intervals, it is not necessary to complete these tasks over the entire data set. The time length you choose, however, should be at least three reoccupation intervals long or 12 hours, whichever is longer.
  • Plot the RMS of the residuals versus base station reoccupation interval. This value should decrease with decreasing reoccupation interval.
  • Discuss the results. Assume base station observations require 10 minutes to complete and regular gravity stations require 5 minutes to complete. Thus, if you were to require a base station reoccupation interval of 2 hours, in 2 hours you could collect 22 gravity stations in addition to the base station observations. If you were to require a base station reoccupation interval of 1 hour, in 2 hours you could collect 20 gravity stations in addition to the base station observations. If you were to require a base station reoccupation interval of every 40 minutes, in 2 hours you could collect 18 gravity stations. What would be your recommendation for the base station reoccupation interval that minimizes the potential of incorrectly accounting for tidal and drift variations while maximizing the cost effectiveness of the survey?
• Observational Error Estimates - To complete this portion of the exercise you will need to download another gravity data set to your computer, import it into a spreadsheet, display the input data using the spreadsheet's display functions, and using the spreadsheet's mathematical functions compute a least-squares best fit line to the data, calculate data point deviations from this best line, and estimate the uncertainty of the data.
  • Download observation error data set to your machine (once redirected, right click the page and select "Save as.." to download the csv file). The first column in the data set lists the time of day in hours and minutes (Hr:mn) that each observation was made, and the second column is the relative gravity reading in mgals. The first line in the data set is a column label line. Columns are tab separated. Clicking on the highlighted area will create a file with the name gerror.dat on your machine.
  • Import gerror.dat into your favorite spreadsheet.
  • Convert the times given to the relative time of each observation from the first observation in minutes. Put these relative times in column 3. That is the time difference between each observation and the first in minutes. Obviously, this will be zero for the first observation and some set of positive numbers for every other observation.
  • Using the graphical features of your spreadsheet, plot the observed gravity versus relative time in minutes. That is, plot column 2 versus column 3. Your plot should resemble, but not exactly, the one displayed above.
  • Compute the least-squares best fit straight line to this data set.
  • In column 4, using the best-fit straight line to the gravity observations, predict what the gravity should have been if there hadn't been any errors in the observations. Do this using the equation you derived above and substitute in the time of the gravity reading appropriate for each observation.
  • In column 5, subtract the predicted gravity value (column 4) from the actual gravity value (column 2).
  • Plot the residual, column 5, versus relative time, column 3.
  • As was done above, compute the RMS of the residual. This value now represents an estimate of the error inherent in each gravity value.
  • Comment on the results.

---

*Residual - Portion of the data set that remains after performing a specific correction. **Wolf, A., Tidal Force Observations, Geophysics, V, 317-320, 1939.