Introduction and Statement of Problem

As is the case in designing a gravity survey, in designing a magnetic survey for a particular application, there are several design parameters that must be chosen or known: magnetic station spacing, location of the base station, and the level of reading error inherent to the basic observations.

Unlike gravimeters, modern magnetometers do not rely on an operator to read or interpolate a dial reading and are relatively insensitive to instrument orientation. Rather, the measured magnetic field strength is displayed digitally or is directly recorded on a field computer. The proton-precession magnetometer typically used in exploration surveys has an inherent reading accuracy of about 0.1 nT. For high resolution work, instruments with a reading accuracy of 0.01 nT are available.

Although the absolute accuracy of the magnetometers is well within the range needed for typical exploration work, magnetic surveys can be plagued by a variety of temporally and spatially varying noises. For example, man-made structures can generate significant magnetic fields that are obviously not related to subsurface geology. These structures can include power lines, bridges, fences, buildings, cars, etc. If possible, magnetic surveys should be conducted away from these features. In addition, the magnetometer operator can produce a measurable magnetic field. As such, the operator can not wear any magnetic material: belt buckles, wire-rimmed glasses, watches, etc. If the proper precautions are taken, and the site well-chosen, the accuracy of magnetic field observations can be reduced to about 1 nT.

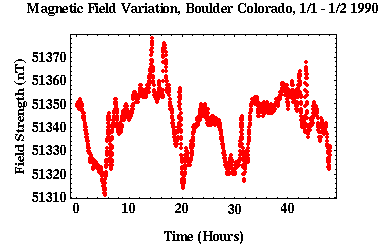
Like gravity measurements, magnetic measurements are time variable. That is, repeated observations made at a given site vary with time. The time variations of importance in exploration surveys are due mostly to external, solar-controlled phenomena. These variations tend to show a diurnal period, like the tidal variations affecting our gravity observations, with an amplitude of about 25 nT. Unlike the tidal variations, however, variations in the strength of the magnetic field can oscillate rapidly and unpredictably. An example of the magnetic field variations observed in Boulder, Colorado is shown above. This example illustrates the field variations that can be expected on a relatively noisy day. Large, external magnetic distrubances, known as magnetic storms, can cause even more erratic variations and in some instances interrupt radio, television, and satellite communications. During times of magnetic storms, all exploration magnetic surveys should be terminated. Magnetic storm forecasts are available. These forecasts are updated 15 minutes past the hour, every hour.

In this exercise we will focus on examining the temporal variations of the magnetic field and on developing strategies for dealing with this variation.

The most obvious way of estimating and eliminating these temporal variations is to incorporate a base station strategy similar to that employed in gravity surveying: establish a base station, periodically reoccupy the base station, remove the time-varying component of the magnetic field by linearly interpolating between base station reoccupation intervals. In using this strategy, time reoccupation interval will be critically important to successfully removing the time varying component of the magnetic field. Unlike the time varying component of the gravity field, however, the magnetic field can vary rapidly with time, thereby necessitating the use of relatively short reoccupation time intervals.

Let's estimate the optimum reoccupation time interval we would have to use to successfully remove the time variable component of the magnetic field. Given the necessary reoccupation interval, does it seem reasonable to use this strategy of noise elimination, or should we consider a different approach?

Procedure

• Base Station Reoccupation Requirements - To complete this portion of the exercise you will need to download magnetic data to your computer, import it into a spreadsheet, display the input data using the spreadsheet's display functions, perform a series of linear interpolations of the data, compute residual estimates between the estimated and actual tidal values, and derive an estimate of the optimal base station reoccupation interval.

To complete this portion of the exercise perform the following tasks:

• Download the magnetic data set to your machine (once redirected, right click the page and select "Save as.." to download the csv file). The first column in the data set is the minute at which the observation was made, and the second column is the absolute magnetic field intensity reading in nT. The first line in the data set is a column label line. Columns are tab separated. Clicking on the highlighted area will create a file with the name 2daysmag.dat on your machine.
• Import 2daysmag.dat into your favorite spreadsheet.
• Using the graphical features of your spreadsheet, plot the observed magnetic field strength versus time. Your plot should resemble the one displayed above.
• Now, determine the effectiveness of a variety of base station reoccupation intervals ranging from 2 hours to 10 minutes.
  • Plot the RMS of the residuals versus base station reoccupation interval. This value should decrease with decreasing reoccupation interval.
  • Discuss the results. In this discussion remember that magnetometers are relatively inexpensive (~$7,500). Therefore, if your required reoccupation interval is short, it may be more cost effective to use two magnetometers: one for recording your survey observations, and one to continuously record the time-variable component of the gravity field at the base station.
    • Using the spreadsheet's mathematical functions, create a third column of data that linearly interpolates the observations between base station reoccupation times. Instead of computing all of the interpolated values between the end points, we will only determine the interpolated value at the midpoint. Usually the interpolation error is greatest at this point. Construct a linear interpolant for the reoccupation interval desired and compute the linearly interpolated value of the magnetic field midway between the interpolation endpoints. Move the end points down one row in the spreadsheet and compute another value. Continue through the entire spreadsheet by pasting this formula down all of column three. These values now represent the time variable component of the magnetic field you would have predicted midway between base station observations recorded at your reoccupation interval. This process will approximate the procedure done in the gravity assignment, but should be much faster to perform.
    • Test how good your predictions are by subtracting the values given in column 3 with the observed magnetic field values given in column 2. Only subtract those values for which you could compute interpolated magnetic observations. You will not be able to compute interpolated values at the beginning or at the end of the spreadsheet using the procedure described above. If your reoccupation interval is appropriate, these residuals should all be small.
    • Plot column 4, the residuals, versus time.
    • To quantify the size of the residual, compute their Root Mean Square value. To compute the root mean square (RMS) residual, do the following: sum the squares of the residuals, divide by the number of residuals used in the sum (do not include the end points used to do the linear interpolation that have zero residual), and take the square root of the result.
    • Repeat these steps for a variety of base station reoccupation intervals. You need to perform this computation over the entire data set. Choose time lengths and intervals that are representative of the data.
  • Reading and Operator Errors - Like the previous exercise, you will need to download a magnetic data set to your computer, import it into a spreadsheet, display the input data using the spreadsheet's display functions, and compute Standard Deviations of the readings. Most spreadsheets have predefined functions that will compute the standard deviation of a set of readings for you. Unlike RMS, which essentially gives you an average magnitude of a set of readings, standard deviation quantifies the spread of readings about some average. The units on the number given as the standard deviation is the same as the units on the numbers used in computing the standard deviation.
    • First, download the magnetic data (once redirected, right click the page and select "Save as.." to download the csv file) collected at mines by GP311 students. This data set is a csv file that can be loaded into your favorite spreadsheet. Its format is, however, more complex than what we've used in the past. Columns in the data set are tab delimited. Choose this option when you load it in.
    • The first block of data represents repeated magnetic readings at a base station and several other stations. The operator name, reading location, reading time, and value of the magnetic field (nT) are listed for six passes along the line. Plot each magnetic profile (the value of the magnetic field at each reading location) one on top of the other.
    • At each reading location, or station, estimate the standard deviation of the magnetic observations. Average these standard deviations together to estimate the reading error associated with magnetic observations.
    • Given this reading error, are there any recognizable magnetic anomalies along the profile?
    • The second block of data represents repeated magnetic observations at two different locations. When collecting these observations, the orientation of the magnetometer was varied and the attitude of the magnetometer was varied from vertical. Analyze these observations and assess the errors associated with instrument orientation.
    • Summarize these results and specify what you think the inherent uncertainty in magnetic observations is based on these data.