Now, the first model we considered consisted of a high velocity layer over a lower velocity half-space, as shown below.

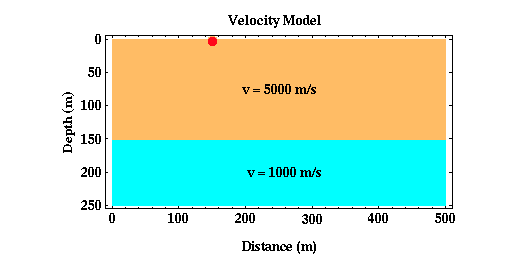
For this model, what first arrivals would you expect to see, and what can you determine about the subsurface structure from these arrivals? A snapshot of the waves produced from a surface source as they interact with the boundary is shown below. This is the same image that was shown previously.

As was described earlier, we need to consider three wave types. The direct arrival, the reflected arrival, and the transmitted (or refracted) arrival. Notice that the difference between the waves produced in this model and those produced when a low velocity layer overlies a higher velocity halfspace is the absence of a head wave.

Let's consider the transmitted (refracted) arrival first. The refracted arrival propagates downward from the boundary. If there is no other structure below our first layer, this wave will continue to move downward. As such, it can never be observed by receivers located on the Earth's surface.

The reflected arrival can be observed on the Earth's surface, but it must always arrive after the direct arrival. Thus, as before, the reflected arrival is never a first arrival, and we therefore do not use it in refraction surveying. The only arrival we'll observe as a first arrival is, therefore, the direct arrival. In this model, the direct arrival propagates away from the source at constant speed (5000 m/s). So, if we were to plot the time of arrival of the first arrivals versus distance from the source, we would get a figure like the one shown below.

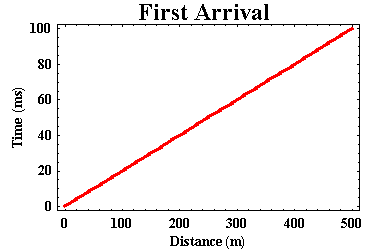
What can we learn from this plot? Well, not too much. From the plot we could compute the speed at which seismic energy travels in the layer, just as we did previously. But notice that our first arrival information no longer tells us anything about the speed at which seismic waves travel in the halfspace. In fact, they no longer indicate any existence of the halfspace!! By this, I mean the travel times shown above would be identical for a uniform Earth that had a wave propagation speed of 5000 m/s.

This example illustrates one of the fundamental limitations of using the seismic refraction method. To be successfully employed (i.e., to get the correct answers from the recorded data), seismic wave speed MUST increase with depth. If wave speed decreases with depth, you will not be able to detect this wave speed decrease. And you will, as a consequence, almost assuredly interpret the first arrivals incorrectly which would result in an estimate of the subsurface structure that is wrong.