For this simple model under consideration, we can compute what the arrival times of the various seismic waves should be and overlay these predicted arrival times on top of our shot record.

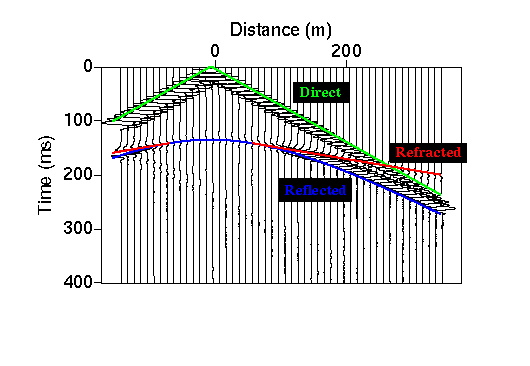
As expected, the first arrival at short offsets is the direct arrival. This arrival has a very large amplitude and its moveout is constant over all offsets. That is, its arrival times fall along a straight line when plotted versus offset. At larger offsets (>275 m), the first arrival is the refracted arrival. This arrival is characterized by small amplitudes and a constant moveout that is smaller in value than the moveout of the direct arrival. That is, the slope of the line connecting the arrival times of the refracted arrival is smaller (the line is flatter) than the direct arrival. The last arrival recorded at all offsets is the reflected arrival. Notice that the reflected arrival does not have a constant moveout at all offsets*. Its moveout is zero at zero offset and it approaches the moveout of the direct arrival at very large offsets.

Plots of the times of arrivals of the various recorded waves versus offset from the source are called travel-time curves. We will often show the travel-time curves of seismic arrivals without overlaying them on shot records as shown below.

Determining the shape of the travel-time curves versus offset will be our primary task in the refraction seismic method. Thus, although we are recording the time history of ground motion at a number of stations, for the refraction method, the only thing we will be interested in extracting from these records is the time of arrival of the first wave to be recorded at each geophone. For the example shown above, this arrival would be associated with the direct wave for offsets less than 275 meters , and it would be associated with the head wave for offsets greater than 275 meters. As we will show later, determining these times from your recorded seismograms is not always easy.