If we include raypaths for the reflected, refracted, and direct arrivals described on the previous page, we would find that a selected set of the raypaths would look like those shown below.

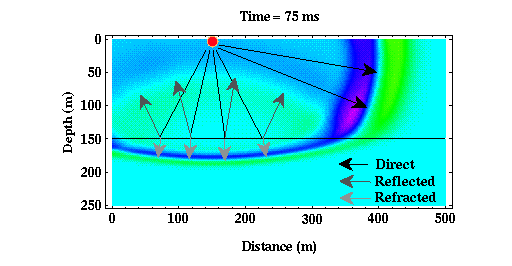
These raypaths are simply drawn to be perpendicular to the direction of propagation of the wavefield at all times. As they interact with the boundary, these raypaths obey Snell's Law. Snell's Law can be derived any number of different ways, but the way it is usually described is that the raypath that follows Snell's Law is the path by which the wave would take the least amount of time to propagate between two fixed points.

Consider the refracted raypaths shown above. In our particular case, v₂, the velocity of the halfspace, is less than v₁, the velocity of the layer. Snell's Law states that in this case, i₂, the angle between a perpendicular to the boundary and the direction of the refracted raypath, should be smaller than i₁, the angle between a perpendicular to the boundary and the direction of the direct raypath. This is exactly the situation predicted by the wavefront's shown in the figure above.

If v₂ had been larger than v₁, a situation we will consider in some detail later, then Snell's Law predicts that i₂ would be greater than i₁. In this case, the wavefront of the refracted wavefield would have smaller curvature than the wavefront of the direct field (in the present case, the wavefront of the refracted field has greater curvature than the wavefront of the direct field).

Snell's law can also be applied to the reflected raypath by setting v₂ equal to v₁. If i₂ is equal to v₁, then the angle of reflection, i₂, should be equal to the angle of the incident wave, i₁, as we would expect from our physics classes. Again, this is exactly the situation predicted by the wavefronts of the reflected wavefield shown above.

As one final note for the case under consideration, for a high velocity layer overlying a low velocity halfspace, the waves described previously and shown above (i.e., direct, reflected, and refracted) are the only body waves observed. Notice also that if we were to place receivers at the Earth's surface, we would never observe the refracted arrival. It continues to propagate downward, never returning to the surface.