Forces Associated with Magnetic Monopoles
Given that the magnetic force applied to one magnetic monopole by another magnetic monopole is given by Coulomb's equation, what does the force look like?
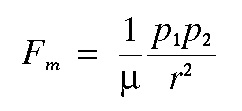
Assume that there is a negative magnetic pole, p1 < 0.0, located at a point x = -1 and y = 0. Now, let's take a positive magnetic pole, p2 > 0.0, and move it to some location (x, y) and measure the strength and the direction of the magnetic force field. We'll plot this force as an arrow in the direction of the force with a length indicating the strength of the force. Repeat this by moving the positive pole to a new location. After doing this at many locations, you will produce a plot similar to the one shown below.
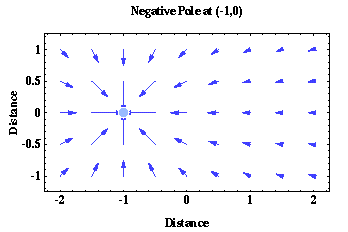
As described by Coulomb's equation, the size of the arrows should decrease as one over the square of the distance between the two magnetic poles* and the direction of the force acting on p2 is always in the direction toward p1 (the force is attractive)**.
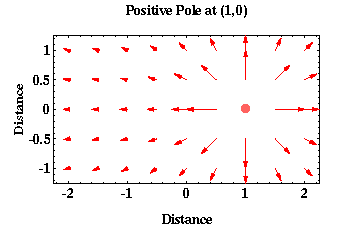
If instead p1 is a positive pole located at x = 1, the plot of the magnetic force acting on p2 is the same as that shown above except that the force is always directed away from p1 (the force is repulsive).
*For plotting purposes, the arrow lengths shown in the figures above decay proportional to one
over the distance
between the two poles rather than proportional to one over the square of the distance between the
two poles. If the true distance relationship were used, the lengths of the arrows would decrease so rapidly
with distance that it would be difficult to visualize the distance-force relationship being described.
** If we were to plot the force of gravitational attraction between two point masses, the plot would look identical to this.